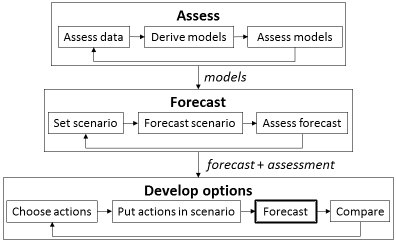
Figure 1. Three types of visual analytics tasks as stages of a single analytical process.
Information Systems, Volume 57, April 2016, Pages 172–194
Video: [Vimeo (good quality)], [YouTube (low quality)]
pre-print: [pdf], published version:
http://dx.doi.org/10.1016/j.is.2015.08.007
Slides: [pdf]
Abstract.
A spatially abstracted transportation network is a graph where nodes are territory compartments (areas in geographic space) and edges, or links, are abstract constructs, each link representing all possible paths between two neighboring areas. By applying visual analytics techniques to vehicle traffic data from different territories, we discovered that the traffic intensity (a.k.a. traffic flow or traffic flux) and the mean velocity are interrelated in a spatially abstracted transportation network in the same way as at the level of street segments. Moreover, these relationships are consistent across different levels of spatial abstraction of a physical transportation network. Graphical representations of the flux-velocity interdependencies for abstracted links have the same shape as the fundamental diagram of traffic flow through a physical street segment, which is known in transportation science. This key finding substantiates our approach to traffic analysis, forecasting, and simulation leveraging spatial abstraction.
We propose a framework in which visual analytics supports three high-level tasks, assess, forecast, and develop options, in application to vehicle traffic. These tasks can be carried out in a coherent workflow, where each next task uses the results of the previous one(s). At the ‘assess’ stage, vehicle trajectories are used to build a spatially abstracted transportation network and compute the traffic intensities and mean velocities on the abstracted links by time intervals. The interdependencies between the two characteristics of the links are extracted and represented by formal models, which enable the second step of the workflow, ‘forecast’, involving simulation of vehicle movements under various conditions. The previously derived models allow not only prediction of normal traffic flows conforming to the regular daily and weekly patterns but also simulation of traffic in extraordinary cases, such as road closures, major public events, or mass evacuation due to a disaster. Interactive visual tools support preparation of simulations and analysis of their results. When the simulation forecasts problematic situations, such as major congestions and delays, the analyst proceeds to the step ‘develop options’ for trying various actions aimed at situation improvement and investigating their consequences. Action execution can be imitated by interactively modifying the input of the simulation model. Specific techniques support comparisons between results of simulating different “what if” scenarios.
On this page you can access high-resolution versions of the figures contained in the paper.

Figure 1. Three types of visual analytics tasks as stages of a single analytical process.

Figure 2. A spatially abstracted transportation network of Milan (Italy) with cell radii about 1km.
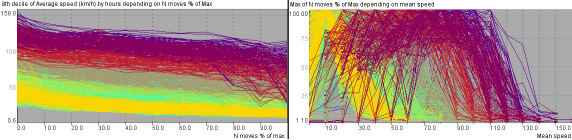
Figure 3. The graphs represent the interdependencies between the traffic intensity and mean speed for the link of the abstracted transportation network of Milan shown in Fig. 2.

Figure 4. The dependencies between the traffic intensity and mean speed can be represented by polynomial regression models.
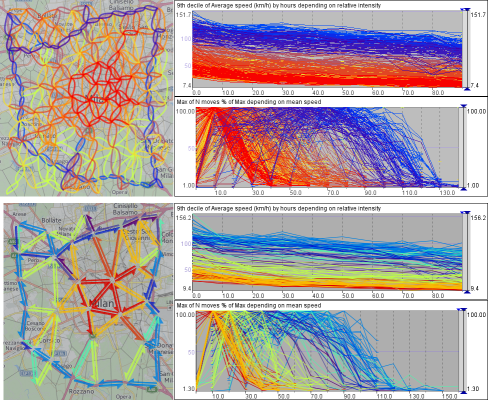
Figure 5. The maps show spatially abstracted transportation networks of Milan with cell radii ? 2km (top) and 4 km (bottom). The graphs to the right of each map represent the dependencies between the relative traffic intensities and the mean speeds on the network links.
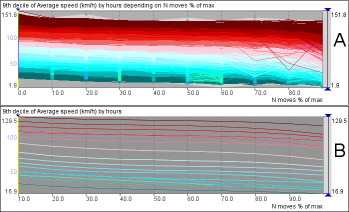
Figure 6. A: The dependency series of the mean speed versus the traffic intensity have been clustered by similarity. B: The dependencies are represented by polynomial or linear regression models.
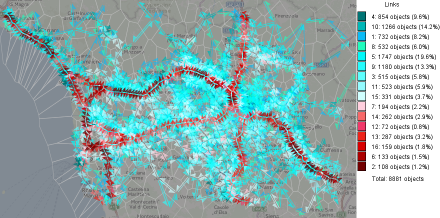
Figure 7. The links are colored according to the cluster membership of the dependencies of the mean speeds on the traffic intensities.
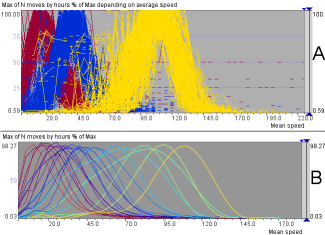
Figure 8. A: Three selected clusters of dependency series of the traffic intensity depending on the mean speed. B: The dependency curves built for all clusters.
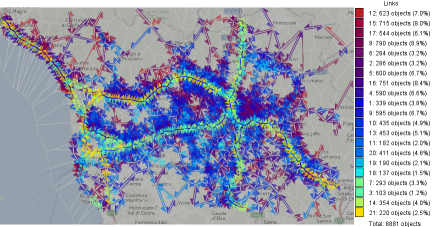
Figure 9. The links are colored according to the cluster membership of the dependencies of the traffic intensities on the mean speeds.

Figure 10. The possible states of vehicles and transitions between the states in the course of the simulation.
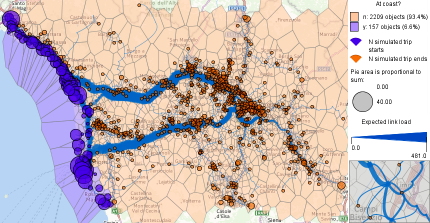
Figure 11. The distribution of the trip origins and destinations and the expected link loads.
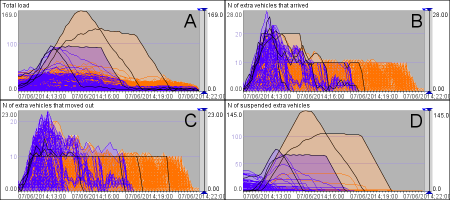
Figure 12. Simulation results aggregated by the places and 10-minutes intervals: total load (A), number of extra vehicles that arrived (B), number of extra vehicles that moved out (C), number of suspended extra vehicles (D). The lines corresponding to the coastal places are shown in violet and the remaining lines in orange.
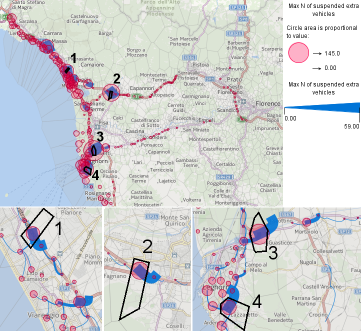
Figure 13. The map shows the places (red circles) and links (blue curved lines) where the evacuating cars will be queuing.
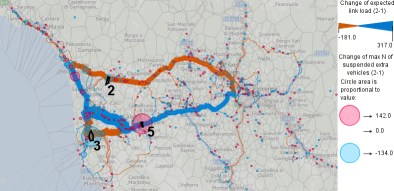
Figure 14. The impact of redirecting a part of the traffic to road SP24 passing Pisa is visualized as a change map.
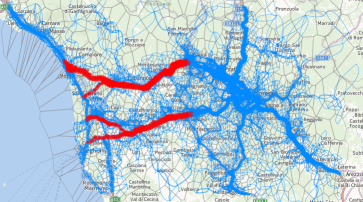
Figure 15. The links where the capacities will be increased by using opposite lanes are shown in red.

Figure 16. The coastal places where some evacuating cars will still be present at 18:00 and later are marked by red circles with the sizes proportional to the numbers of these cars.
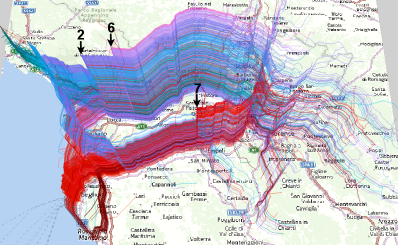
Figure 17. The simulated car trajectories are represented in a space-time cube. The arrows point at the places of major suspensions.
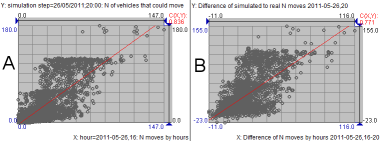
Figure 18. A: The relationship between the real flows in hour 16 (X-axis) and the simulated flows for hour 20 (Y-axis). B: The relationship between the differences of the real flows in hour 16 from hour 20 (X-axis) and the differences of the simulated flows from the real flows in hour 20 (Y-axis).
Last updated: August 13, 2015